נבחן את התנאי להתאבכות בנקודה P_m.

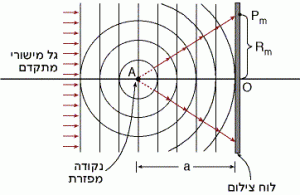
איור 10.4: התאבכות בין גל כדורי ממקור נקודתי, עם גל מישורי.

לנוחיות ההסבר, נניח גם שבנקודה O מתרחשת ביניהם התאבכות בונה.

תנאי להתאבכות בונה בנקודה P_m:

התאבכות בונה בנקודה P_m על הפילם, תתקיים כאשר קיים הפרש דרכים מנקודה A שהוא כפולה שלמה (m=1,2,3,4,…) של אורך הגל (λ):

AP_m-AO = mλ,

AO = a

על הפילם מתקבלים מעגלים קונצנטריים כמו שמקבלים בניסוי בעקיפה בחריר עגול.

רדיוסי המעגלים ניתנים על פי משפט פיתגורס:

a²+R_m² = (a+mλ)² = a²+2maλ+m²λ²

כאשר מחלצים את הרדיוסים, מקבלים:

R_m² = λ*(2ma+m²λ)

מכיוון שאורך הגל (l) קטן בהרבה (סידרי גודל) מהמרחק בין המקור לפילם (a), ניתן להזניח את הביטוי השני המופיע בסוגריים, ומקבלים:

R_m² = 2mλa

מנוסחה זו רואים כי היחסים בין ריבועי רדיוסים עוקבים, הם יחסים בין מספרים שלמים עוקבים.

קיבלנו סידרת טבעות של אור וחושך על פני הפילם.

לאחר פיתוח הפילם על שקף, מקבלים שקף בו האזורים שנוצרו מטבעות האור הם שקופים, והאזורים שנוצרו מטבעות החושך כהים. תמונה זו נקראת:

Fresnel Zone Plate (לוח אזורי פרנל)