הערה: במידה ואתם נתקלים בבעיות Security, שאינן מאפשרות להריץ את ההדמיות באתר זה, אנא התייחסו לנתון הבא:
החל משנת 2014, חברת אוראקל, ביצעה עידכון של תוכנת ג'אווה, המותקנת במחשבים. כתוצאה מכך, ההדמיות של אתר זה, אינן ניתנות להרצה במחשב המשתמש, ללא השינוי המוסבר בהמשך.
הוראות לתיקון הבעיה, כך שניתן יהיה בקלות להריץ את ההדמיות, נמצאות בהוראות בעמוד רשימת הדמיות ג'אווה באתר.
בפועל, ביצוע הוראות אלו, מחזיר את המערכת לפעולה, כפי שהייתה נהוגה כברירת מחדל, עד לעדכון ג'אווה זה.
לפני הפעלת כל תכנית ג'אווה, המערכת שואלת את המשתמש, האם הוא מאשר להריץ אותה.
סיפור המסגרת – מתוך הספר של פיינמן (1):
אתה יושב על חוף אגם, ורואה מרחוק אדם טובע.
ברצונך להציל אותו!
הזמן הוא גורם קריטי ! – הנך חייב להגיע אל הטובע מהר ככל האפשר (מסלול בו זמן התנועה מינימלי).
עליך להחליט מהו המסלול המהיר ביותר אל הטובע?
הפעלת היישומון של עקרון פרמה:
הקלקה על לחצן שמאלי של העכבר קובעת את מיקום נקודת ההתחלה בתווך n1.
הקלקה על לחצן ימני של העכבר קובעת את מיקום נקודת הסיום בתווך n2.
באפשרותך לשנות את מקדמי השבירה של התווכים n1 ו n2.
לחיצה על כפתור Go מפעילה את ההדמיה ביישומון.
ניתוח פיזיקלי של הבעיה:
מהירות התנועה בחול שונה ממהירות התנועה במים.
ברור כי באותו תווך עליך לנוע בקו ישר (מדוע?).
מהירותך בחול על החוף שווה למהירותך המכסימלית מחולקת בגודל n1 של תווך החוף.
מהירותך במים שווה למהירותך המכסימלית מחולקת בגודל n2 של תווך האגם.
הבעיה היא למצוא את הנקודה על הגבול בין התווכים בה עליך לעבור מתווך אחד לשני. בנקודה זו משתנה כיוון התנועה (אלא אם כן שני התווכים בעלי n שווה, או שהטובע נמצא באותו x כמוך).
פייר פרמה (1650) קבע את עקרון הזמן האקסטרמלי:
"אלומת אור הנעה מנקודה לנקודה תעבור במסלול הזמן המינימלי (אקסטרמלי) (ביחס לנקודות השכנות) בין שתי הנקודות".
באיור שלפניך מופיעה הבעיה עם הפרמטרים הקובעים את התנהגותה.
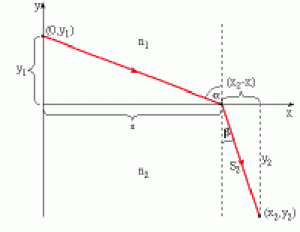
איור 1: מערכת קואורדינטות לתיאור מקרה התנועה על פי עקרון פרמה.
מהירות היא דרך מחולקת בזמן:
![]()
מהירות תנועה בתווך היא מהירות התנועה המכסימלית (c) מחולקת בגודל אופייני לתווך n:
![]()
מכאן הזמן ניתן על ידי:
![]()
זמן התנועה הכולל בשני התווכים:
![]()
על פי משפט פיתגורס ניתן לחשב את זמן התנועה הכולל, כפונקציה של פרמטר אחד בלבד (נקודת הפגיעה x במשטח הגבול בין שני התווכים):
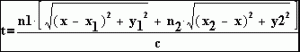
כדי למצוא זמן מינימלי, יש לגזור את המשוואה, ולהשוות לאפס.
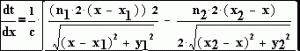
התוצאה המתקבלת היא:
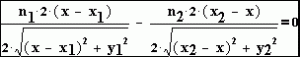
זהו גם חוק סנל באופטיקה (לשבירת אור במעבר בין שני תווכים):
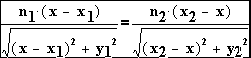
ניסיון לפתור שוויון זה יצר משוואה ממעלה רביעית (!).
פיתרון אנליטי של משוואה זו היה מסובך, ולכן נעזרתי בתוכנת "מתמטיקה" כדי להגיע לפיתרון (בעזרתו האדיבה של ברנט סרינג מבית הספר למדעים ואומנויות בירושלים). הפיתרון הוא לא ריאלי ליישום, אך אם ברצונך לראות אותו, עליך להצטייד תחילה בתוכנת MathReader אותה ניתן להוריד בחינם מהכתובת:
אם ברשותך תוכנת הצפייה MathReader, הקלק כאן (הקובץ נקרא Ferma1.nb).
שאלות:
- עבור שני תווכים נתונים, איזה ערך נשאר קבוע?
- האם ערך קבוע זה תלוי במיקום נקודת ההתחלה? נקודת הסיום?
- האם עקרון פרמה קשור בדרך כלשהי לזווית קריטית?
לפני שנים רבות נכתבה על ידי דוד זינגר במחלקה להוראת המדעים במכון ויצמן למדע פעילות ממוחשבת (למחשבי XT) על עקרון פרמה. למרות שפעילות זו פועלת במערכת הפעלה DOS, ואינה צבעונית, יש בה אספקטים פדגוגיים המצדיקים שימוש בה גם כיום. באם ברצונך לטעון פעילות זו למחשבך, הקלק כאן.

