לכל המפתחות שהכרנו, שתי תכונות:

• סימטריה: מפתח ההצפנה זהה למפתח הפענוח ופעולת הפענוח הפוכה לפעולת ההצפנה. מתכונה זו נובעת תכונה נוספת:
• סודיות: כיוון שמפתח ההצפנה והפענוח זהים, מפתח ההצפנה מוכרח להיות סודי. גם אם מניחים ששיטת ההצפנה אינה סודית, המפתח עצמו ידוע אך ורק לשולח המסר ולנמען. חשיפת המפתח על ידי האויב, מגלה את המסר ומחסלת את אבטחת המערכת.

כל מערכות ההצפנה הקלאסיות, שהיו בשימוש יותר מאלפיים שנה, מבוססות על מפתחות סימטריים, ולכן בהכרח סודיים וזה גם מקור המגבלות שלהן.

מגבלות ההצפנה הסימטרית

1. הצורך בהסכם מוקדם בין השולח לנמען: הצפנת המסרים בשיטה הסימטרית, מחייבת את השולח ואת הנמען להסכים מראש על המפתח. במערכות הצפנה כאלה, כדי להסכים על המפתח, יש הכרח בהתקשרות מקדימה בין השולח (המצפין), לבין לנמען, בערוץ חסוי ומאובטח, עוד לפני העברת המסר עצמו. אבל אחת הבעיות בעולם התקשורת, הוא המרחק הרב בין השולח לנמען. המרחק הרב מקשה מאוד על ביצוע "ההסכם המוקדם", על מפתח סודי משותף לשולח ולנמען, כך שלא יתגלה על ידי גורם לא רצוי.
2. ריבוי המפתחות: במערכת הצפנה סימטרית: לכל זוג של משתמשים, יש מפתח הצפנה משלו. זהו המפתח שישמש את הזוג במהלך ההצפנה וגם במהלך הפיענוח.

כמה מפתחות דרושים למערכות הצפנה סימטריות רבות משתמשים?

שני משתמשים זקוקים למפתח אחד. לכמה מפתחות זקוקים שלושה משתמשים (א', ב', ג')? נניח שהסכם מפתח דינו כלחיצת יד. א' לוחץ יד עם ב' ו- ג' (בוצעו הסכמים על שני מפתחות), ב' ו- ג' לחצו ידיים (בוצע הסכם מפתח נוסף). בסך הכול, שלושה משתמשים, שכל אחד מהם מעוניין לתקשר עם שני האחרים, זקוקים לשלושה מפתחות.
מה במקרה הכללי של n משתמשים שכל אחד מהם מעוניין לתקשר בהצפנה עם כל האחרים? הראשון מסכים על מפתחות עם n-1 המשתמשים האחרים (כולם פרט לו עצמו). על כמה מפתחות נותר למשתמש השני להסכים? עם המשתמש הראשון הוא כבר הסכים על מפתח. עם עצמו אין לו צורך להסכים. לכן נותרו n-2 משתמשים, שעליו להסכים אתם על מפתחות הצפנה. מאותם שיקולים למשתמש השלישי נותר להסכים על n-3 מפתחות, לרביעי על n-4 וכך הלאה. כשהגענו למשתמש השלישי מן הסוף, עם כמה משתמשים נותר לו להסכים על מפתח? רק עם שני האחרונים. השני מן הסוף? רק עם אחד, עם האחרון. אז על כמה מפתחות הוסכם בסך הכול?

( 1+2+3+… + ( n-4)+(n-3)+(n-2)+(n-1)

זהו מספר המפתחות להם זקוקים n משתמשים, כדי לתקשר ביניהם ללא מגבלה (כל אחד עם כל האחרים).

• כיצד לחשב מספר זה?

כדי להקל על החישוב נחבר את אברי הסדרה בזוגות:

האיבר הראשון עם האחרון:

 n = (n-1)+1

האיבר השני עם האיבר השני מן הסוף:

 n = (n-2)+2

האיבר השלישי עם האיבר השלישי מן הסוף:

 n = (n-3)+3

וכך הלאה, עבור כל איברי הסדרה.

סכום כל אחד מהזוגות שיצרנו הוא n.

• כמה זוגות כאלה יש?  מחצית ממספר אברי הסדרה:

 (n-1)/2

מכאן מקבלים כי הסכום של כל איברי הסדרה שווה למכפלה של ערכו של כל זוג (n), במספר הזוגות. מכאן שהמספר הכולל של המפתחות במערכת סימטרית הוא:

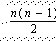
כדי לדון במשמעות של העובדה הזאת, השלימו את הטבלה הבאה:

מספר משתתפים בהצפנה סימטרית	מספר המפתחות לו הם זקוקים
10
50
100
500
1000
50000
100000
1000000
N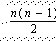

אנחנו רואים לפי החישובים בטבלה, כי מיליון משתמשים זקוקים ל:

ובמילים, מיליון משתמשים במערכת הצפנה סימטרית, זקוקים לחמש מאות מיליארד מפתחות. מיליון משתמשים זה מספר סביר כשמדובר ברשתות אינטרנטיות. אבל ניהול של 500 מיליארד מפתחות הוא בלתי ישים לחלוטין.

לסיכום, שתי הבעיות, בעיית ההסכם המוקדם ובעיית ריבוי המפתחות, הן המגבלות של מערכות הצפנה סימטריות. הן הופכות את ניהול מערכת המפתחות למשימה מסובכת מאוד וכשהמערכת רבת משתמשים, לבלתי ישימה. שורש הבעיה בסימטריות של המערכת.

• האם קיימת אפשרות אחרת?
• האם אפשר לפתח מערכות הצפנה אחרות, שלא יסבלו ממגבלות אלה?