המטרה העיקרית של תכנית אגם לחינוך חזותי היא לעזור לילדים צעירים לשפר את התפתחותם הקוגניטיבית והרגשית, ע"י פיתוח השפה החזותית. פרויקט זה מהווה דוגמה של שיתוף פעולה יוצא דופן בין אמן ומכון מחקר: האמן יעקב אגם יזם וכתב את התוכנית (אגם, 1984, 1981). התוכנית נהפכה למציאות חינוכית ע"י מחקר ופיתוח של צוות פרויקט אגם, במחלקה להוראת המדעים במכון ויצמן למדע. בשנים 1984- 1990 התכנית הופעלה לראשונה עם ילדים בני 3 עד 5. חלק מקבוצות הילדים המשיכו לעבוד עם התכנית עד לכיתה ג'. מחקר והערכה ליוו את הפיתוח וההפעלה באותן השנים.

(Razel & Eylon, 1986; 1990; Eylon & Rosenfeld, 1990; Hershkowitz & Markovitz, 1992; Markovitz & Hershkowitz, 1996, Hershkowitz, Parzysz & van Dormolen, 1996).

בשנת 1996 זכה יעקב אגם בפרס ע"ש קומיניוס מטעם אונסקו. פרס יוקרתי זה נועד לתת כבוד לחדשנות בחינוך. הפרס הכיר גם בחדשנות התוכנית וגם במחקר החינוכי המלווה.
פעילות הפרויקט פסקה מחוסר מימון, למרות התוצאות המבטיחות של המחקר וההערכה. בשנת 2005, בעקבות תמיכתו ועידודו של משרד החינוך, חודשו הפיתוח, ההפעלה והמחקר בתכנית. התכנית מופעלת כעת על ידי צוותים במחלקה להוראת המדעים במכון ויצמן למדע ובמכללת אורנים ליד חיפה. התכנית מופעלת בכ- 100 כיתות גן ובמספר כיתות א'- ג' בבתי ספר אחדים בארץ.
פיתוח נוסף של התכנית תופס מקום חשוב בפעילות הפרויקט.
התכנית מתקבלת בהתלהבות רבה על ידי תלמידים, מורים והורים במקומות בהם היא מופעלת.

הדוגמה הבאה מדגימה כיצד חשיבה ויזואלית מתפתחת בתכנית אגם:
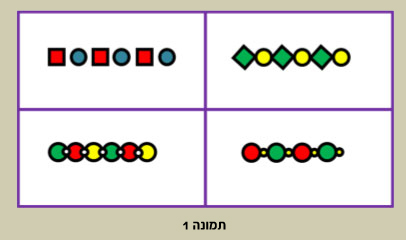
על ידי שימוש במעגלים ובריבועים כ"אותיות ויזואליות" , יוצרים הילדים "תבניות" (PATTERNS), אשר הן "מילים ויזואליות" או "משפטים ויזואליים" (החוברת "עיטורים", המציגה את התבניות, היא היחידה השלישית בתכנית). "תבנית", במובן שבו משתמשים בתכנית אגם, היא בעצם סידרה ויזואלית מחזורית שמרכיביה, בשלב זה של התכנית, הם עיגולים וריבועים, במידות, בצבעים ובכיוונים שונים, עם רווחים משתנים ביניהם (ראה תמונה 1).

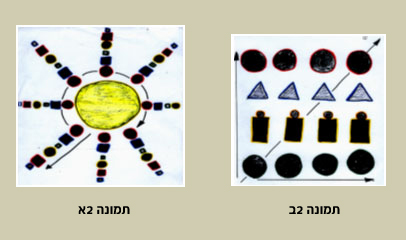
סדרות מחזוריות הינן בסיס למושגים מדעיים ומתמטיים רבים: כמו פונקציות, גלים ותנועות. יחידה זו מדגימה את המושג בצורה ויזואלית ובדרך משמעותית לילדים הצעירים. ביחידת התבניות כל הפעילויות עוסקות בתבניות לינאריות (מימד אחד), אבל יצירתיות הילדים אינה יודעת גבול. ראה למשל, את ה"שמש", בתמונה 2א, שבה הילד יצר סידרה מחזורית בשני מימדים, כאשר כל קרן מהווה את הנושא המחזורי של "סידרת השמש", וכל קרן בעצמה היא תבנית מחזורית לינארית. המטריצה היא דוגמה נוספת לתבנית רב מימדית שנוצרה על ידי ילדים; כל שורה, כל עמוד, ושני האלכסונים הראשיים מייצגים תבנית לינארית, וכל המטריצה היא תבנית עם העמוד (השורה) כנושא מחזורי (ראה תמונה 2ב).