זיהוי נתונים ומסקנות - משימטיקהמשימטיקה

מטרות התיק
רקע
הצעה למהלך העבודה
זמני עבודה משוערים
החומרים והעזרים הדרושים – להורדה
פתרונות של תלמידים

מטרות התיק

לסייע למורה להעריך את יכולת התלמידים לזהות מה הנתונים (ההנחות) ומה המסקנה, בהינתן טענה גאומטרית.

ההערכה והמענה לקשיים מתמקדים ביכולת התלמידים:

לכתוב בכתיב מתמטי נתונים ומסקנות, בהינתן טענה גאומטרית המנוסחת במילים.
לנסח במילים טענה גיאומטרית המנוסחת בכתיב מתמטי.

רקע

הוכחה והפרכה של טענות היא פעילות מרכזית בכל ענפי המתמטיקה. טענות מתמטיות בכלל, וגיאומטריות בפרט, מנוסחות לעיתים במילים ולעיתים בכתיב מתמטי. דרכי הניסוח השונות מציבות קשיים שונים בפני התלמידים.

כאשר טענות מתמטיות מנוסחות במילים, תלמידים רבים מתקשים לזהות את ההנחות שבבסיס הטענה ואת המסקנה שהטענה קובעת על סמך הנחות אלה. בגיאומטריה מקובל לתאר קושי זה, כך: זיהוי מה נתון ומה צריך להוכיח (או להפריך). זיהוי כזה הוא חיוני לצורך הוכחת טענה נתונה (או הפרכתה). לדוגמה, כשנתונה הטענה אם משולש הוא שווה שוקיים, אז הגובה לבסיס הוא גם תיכון, יש תלמידים המתקשים לזהות שהנתונים (הנחות הטענה) ומה שצריך להוכיח(המסקנה) הם:

נתונים:

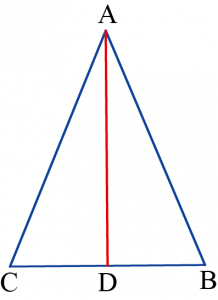במילים: משולש, שוויון בין אורכי שתי צלעות במשולש, גובה לצלע השלישית

או

בכתיב מתמטי: \(\displaystyle \Delta ABC\) (ראו שרטוט)

\(AB=AC\)

\(AD\bot BC\)

צריך להוכיח:

במילים: הגובה חוצה את הצלע השלישית

או

בכתיב מתמטי: \(BD=CD\)

אחד הגורמים לקושי לזהות מה נתון ומה צריך להוכיח נעוץ בצורך לכתוב נתונים ומסקנות בכתיב מתמטי, בהינתן טענה גיאומטרית המנוסחת במילים. לדוגמה, קושי לרשום \(\displaystyle \Delta ABC\), \(AB=AC\) וכו' בטענה הנ"ל. גורם אפשרי נוסף נעוץ בצורך לזהות נתונים כאשר הם אינם מופיעים בחלק הראשון של הטענה. לדוגמה, ישנם תלמידים שאינם מזהים שהגובה לבסיס הוא אחד הנתונים בטענה שלמעלה, מאחר והוא מופיע בחלק השני של המשפט המנוסח במילים.

כמו כן, כאשר טענה גיאומטרית מנוסחת בכתיב מתמטי, תלמידים רבים מתקשים להבין ולנסח אותה במילים. לדוגמה, לזהות שהנתון \(AD\bot BC\) בדוגמה למעלה פירושו גובה לבסיס, ושהנתונים \(\displaystyle \Delta ABC\) ו-\(AB=AC\) פירושם שהטענה טוענת משהו על משולש שווה שוקיים, ומכאן שאת מכלול הכתיב המתמטי בדוגמה לעיל ניתן לנסח במילים באופן הבא: אם משולש הוא שווה שוקיים, אז הגובה לבסיס הוא גם תיכון, או הגובה לבסיס במשולש שווה שוקיים הוא גם תיכון, וכד׳.

התיק זיהוי נתונים ומסקנות, נועד לסייע למורה לזהות תלמידים המתקשים לרשום בכתיב מתמטי את הנתונים והמסקנה כאשר הטענה מנוסחת במילים, או לנסח במילים טענה הרשומה בכתיב מתמטי, ולתת להם מענה.