- מטרות התיק
- רקע
- הצעה למהלך העבודה
- זמני עבודה משוערים
- החומרים והעזרים הדרושים – להורדה
- פתרונות של תלמידים
מטרות התיק
לסייע למורה להעריך את יכולת התלמידים לקשור בין שימוש בדוגמאות פרטיות לבין הוכחות והפרכות של טענות גיאומטריות. התיק עוסק בנושא מרובעים.
ההערכה והמענה לקשיים מתמקדים ביכולת התלמידים:
- לפסול הוכחות לנכונות טענות לגבי מרובע כלשהו, המתבססות רק על דוגמאות פרטיות.
- להשתמש בשיטה של דוגמה נגדית כדי להוכיח שטענה לא נכונה.
- לזהות דוגמאות פרטיות שיכולות לשמש כדוגמאות נגדיות לטענות לא נכונות.
רקע
במתמטיקה עוסקים רבות בבחינת אמיתות של השערות, במטרה להוכיח או להפריך אותן. שיטה נפוצה להפרכת טענות במתמטיקה היא מתן דוגמה נגדית. שיטה זאת מתבססת על כך שבמתמטיקה טענה נחשבת נכונה אם ורק אם היא נכונה תמיד, כלומר, היא חלה על כל מקרה פרטי. לכן, די במקרה פרטי אחד שלגביו טענה אינה נכונה, כלומר, די בדוגמה נגדית אחת, כדי לפסול נכונות של טענה ובכך להפריכה.
תלמידים מתקשים לעיתים קרובות בשימוש בשיטה של דוגמה נגדית לצורך הפרכה של טענות. קושי זה כרוך הן בהכרה בשיטה זאת כמתאימה להוכחה שטענה איננה נכונה, והן בזיהוי וביצירה של דוגמאות נגדיות.
קושי נפוץ נוסף של תלמידים הוא שימוש בדוגמאות פרטיות בהקשר של הוכחות במתמטיקה, אך לא לצורך הוכחה שטענה מסוימת אינה נכונה, אלא לצורך הוכחה של טענה כללית. לדוגמה, הטענה גבהים לצלעות סמוכות במעוין שווים באורכם, היא טענה נכונה, אך כדי להוכיח את הטענה, לא מספיק לבנות באמצעות המחשב מעוינים, ולשרטט גבהים לצלעות סמוכות. בכל המקרים האלה הגבהים אכן שווים באורכם (ראו שרטוטים למטה) אבל השימוש בדוגמאות אינו מהווה הוכחה לנכונות הטענה.
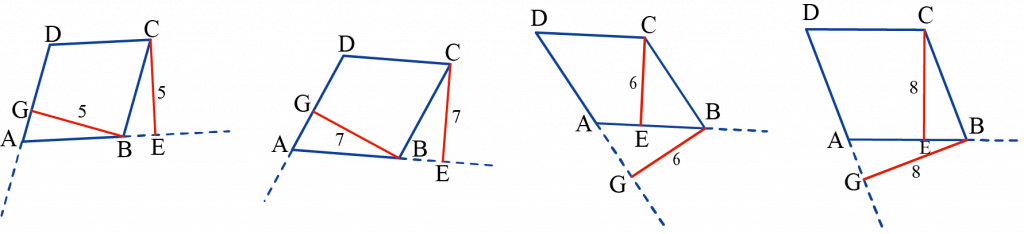
נושא המרובעים הוא נושא מרכזי בתוכנית הלימודים בגיאומטריה. התיק דוגמה נגדית: מרובעים נועד לסייע למורה לזהות תלמידים המתקשים בשימוש במקרים פרטיים בהקשר של הוכחות והפרכות של טענות גיאומטריות, ולתת להם מענה.
הצעה למהלך העבודה
- עבודה על משימות הערכה:
- משימה 1: בודקים הסברים.
- משימה 2: מפריכים טענה שאינה נכונה.
- משימה 3: בוחרים דוגמאות נגדיות.
- הערכת תוצרי התלמידים.
- פעילויות דיפרנציאליות בעקבות ההערכה.
זמני עבודה משוערים
-
- עבודה על משימת ההערכה: 30-20 דקות.
- פעילויות בעקבות ההערכה: 90-60 דקות.
החומרים והעזרים הדרושים
לצורך העבודה על משימות הערכה (לכל תלמיד/ה):
- דף משימה 1: בודקים הסברים.
- דף משימה 2: מפריכים טענה שאינה נכונה.
- דף משימה 3: בוחרים דוגמאות נגדיות.
לצורך הערכת תוצרי תלמידים:
לצורך הפעילויות בעקבות ההערכה (לכל תלמיד/ה):
- לפעילות 1
- דף פעילות 1: האם ההסברים משכנעים?
- היישומון: "גבהים במעוין".
- לפעילות 2
- דף פעילות 2: מפריכים טענות באמצעות דוגמאות נגדיות.
- היישומון: "זוג צלעות מקבילות וזוג זוויות סמוכות שוות" .
- היישומון: "האם האלכסונים במלבן מאונכים?"